Plastron Lubrication Model
The terminal velocity of a slowly rising bubble of gas in clean water does not obey the same rules as the terminal velocity of a solid sphere falling slowly in clean water. This is because the flow of water past the bubble “rubs” its surface and sets the gas into a recirculating motion. The bubble has less drag because it can ease its way through the water. Hadamard-Rybzinski drag governs the drag of bubbles unless their surfaces are rigid (in which case Stoke’s drag applies). The same effect can ease flow past solid spheres and across solid surfaces.
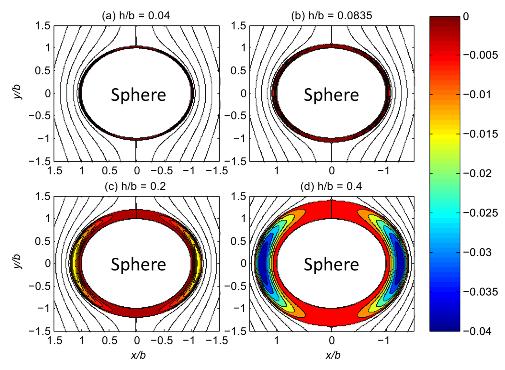
Flow past a solid sphere with different thickness layers of air.
The image above (taken from publication [1] below) shows calculated streamline patterns illustrating this circulation in the plastron layer (the shaded contours) for different values of the plastron thickness (h/b). Because a thin air layer cannot easily have an internal recirculation and a thick air layer obstructs the flow, there is always an optimum thickness of air layer, as shown in the graph below (taken from publication [2] below).
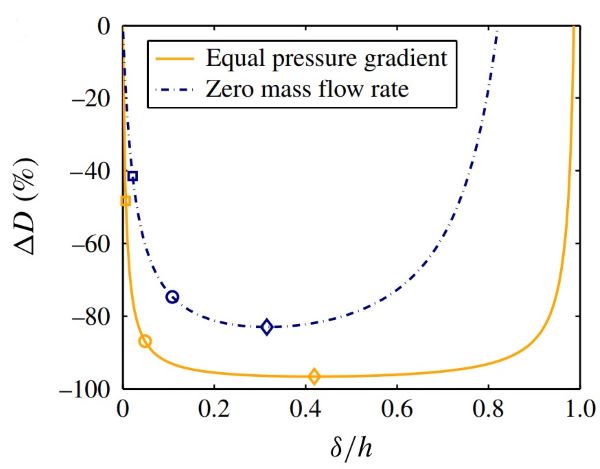
Change in drag ∆D, as a function of the relative thickness of the gas layer, ẟ/h.
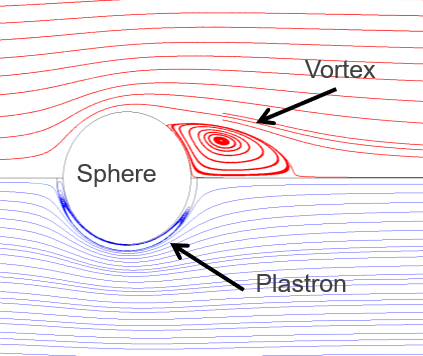
Our analytical models of the drag on an air encapsulated sphere at creeping flow predicts an 18% drag reduction in water. Numerical models predict that when the flow rate is increased the reduction in drag will be dramatic due to the suppression of vortices and the reduction in the wake (see below). The same ideas can be applied to flow in channels and tubes. A recirculating layer of air between the solid and the liquid can lubricate the flow of the core liquid.
Publications
- Plastron induced drag reduction and increased slip on a superhydrophobic sphere G. McHale, M.R. Flynn and M.I. Newton, Soft Matter 7 (2011) 10100-10107.
- Change in drag, apparent slip and optimum air layer thickness for laminar flow over an idealised superhydrophobic surface A. Busse, N.D. Sandham, G. McHale and M.I. Newton, J. Fluid Mech. 727 (2013) 488-508.
See also the Journal Focus on Fluids article. - Simulations of laminar flow past a superhydrophobic sphere with drag reduction and separation delay B.R.K. Gruncell, N.D. Sandham and G. McHale, Phys. Fluids 15 (2013) art. 043601.
