Liquid version of Young’s Law
A droplet on a SLIPS rests on a layer of lubricating liquid rather than directly on the underlying solid. As a consequence, the shape of the droplet profile near the solid surface is different to that of a droplet resting directly on the solid because the droplet “pulls up” some of the lubricant around it.
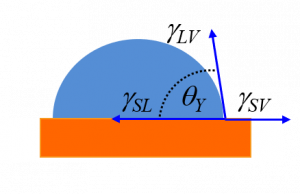
On a rigid solid surface, the contact angle ϴY between the droplet and the surface is related to the interfacial surface tensions ƔSL, ƔSV and ƔLV at the solid-liquid, solid-vapour and liquid-vapour interfaces respectively through Young’s law (also called Young’s Equation):
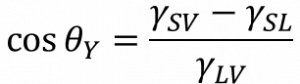
However, when the droplet is on a lubricating layer such as oil, the apparent contact angle ϴapp is different to the contact angle ϴY on a solid surface.

Mathematically, in the limit of a thin lubricating layer, the apparent contact angle is defined by the liquid equivalent of Young’s law:
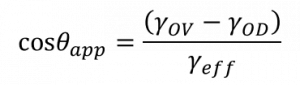
where ƔOV and ƔOD are the interfacial surface tensions at the oil-vapour and oil-droplet interfaces respectively, and Ɣeff is an effective surface tension. This is equal to ƔDV if the oil (or other lubricating fluid) simply spreads part-way up the side of the droplet, as in the image below.
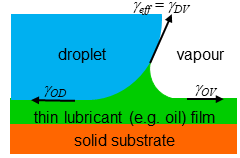
However, the droplet can also become cloaked in oil, as in the image here:
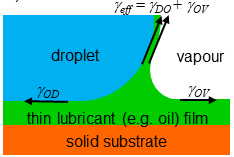
In this case, the effective surface tension is ƔDO+ ƔOV.
The predictions made by the liquid version of Young’s law agree well with experimental measurements for thin lubricating layers. The image below shows a droplet with a thin silicone oil-infused superhydrophobic nanoparticle coating on a glass substrate. The apparent contact angle predicted by the liquid form of Young’s law is between 106.1° and 108.4° (depending on the values taken for the interfacial surface tensions) whereas the experimental value is 108.4°.

For thicker layers, the predicted value is an upper bound for the experimental value.
Publications
- Apparent contact angle and contact angle hysteresis on liquid infused surfaces, C. Semprebon, G. McHale and H. Kusumaatmaja, Soft Matter 13 (2017), 101-110
- Apparent contact angles on lubricant-impregnated surfaces/SLIPS: From superhydrophobicity to electrowetting, G. McHale, B.V. Orme, G.G. Wells and R. Ledesma-Aguilar, Langmuir 35 (2019), 4197–4204
