Nature's Raincoats

Liquid-on-Solid Amontons’ Laws

We know that there is resistance when we try to push or drag a solid object across a solid surface. This is known as friction. Here, we show that there are direct analogies between the description of friction between two solids and friction between a solid and a liquid.

Friction between two (dry) solid bodies can be described by empirical laws that date back to the work of Amontons in 1699, and are predated by work of Leonardo da Vinci. Fundamental to those laws are the concepts of static and kinetic coefficients of friction. These relate the pinning and sliding friction forces along a surface to the load force normal (perpendicular) to the surface, as shown in the Figure below.

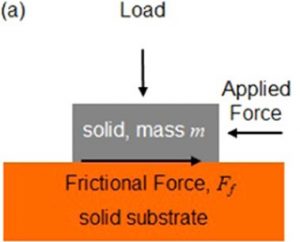
More specifically, Amontons’ first two laws of dry friction state that for any two solid materials, the lateral friction force, F_f, is directly proportional to the normal applied load, F_N, with a constant of proportionality, the friction coefficient μ, that is independent of the contact area. In other words,

F_f = μF_N

This makes sense because we know it is much easier to push an object across an ice rink than it is to push the same object across rough ground. The coefficient of friction μ for ice is smaller than for the rough ground, meaning that the force required to overcome the frictional force F_f is less.

For liquids on solid surfaces, contact lines also experience pinning, and the language of friction can used when droplets are in motion. Recently, it was argued that droplet-on-solid friction can be separated into a static and a kinetic regime, similar to solid-on-solid friction [1].

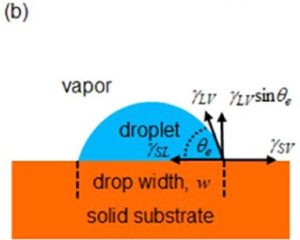
Surface free energy considerations can be used to show that the frictional force per unit length of a contact line is directly proportional to the normal component of the surface tension force [2]. Coefficients of friction can be defined for both contact lines and droplets that provide a droplet analogy of Amontons’ first and second laws. Here, the normal load force of a solid is replaced by the normal surface tension force of a liquid. In the static regime, the coefficient of static friction, defined by the maximum pinning force of a droplet, is proportional to the contact angle hysteresis. This is shown in Figure (b) below.

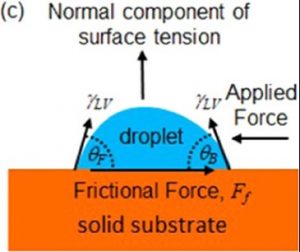
In the kinetic regime, the coefficient of kinetic friction is proportional to the difference in dynamic advancing and receding contact angles. This is shown in Figure (c) below.

Publications

1. How drops start sliding over solid surfaces, N. Gao, F. Geyer, D. W. Pilat, S. Wooh, D. Vollmer, H.-J. Butt and R.Berger, Nature Physics 14 (2018), 191–196
2. Friction coefficients for droplets on solids: The liquid–solid Amontons’ laws, G. McHale, N. Gao, G.G. Wells, H. Barrio-Zhang and R. Ledesma-Aguilar, Langmuir 38 (2022), 4425-4433