Controlling Instabilities
Toroidal films
We have seen here that we can create electric field patterns in geometric shapes that allow us to create novel liquid shapes. We can see further interesting effects by defining field patterns with complex topologies. In particular, we have studied the dewetting of liquids placed in an electric field that defines a toroidal film. This is different to the cases we looked at previously because of the hole in the middle of the toroidal film. A torus is an example of a shape which is not simply connected. This means that paths through the shape can’t all be contracted to a point.
Liquid that has been pulled out into a toroidal film will initially keep its toroidal shape during dewetting after the voltage is removed. However, the toroidal shape proves to be unstable. What happens next depends upon both the volume of liquid deposited and the aspect ratio of the toroidal film, which we define to be the ratio of the mean radius of the film divided by the mean width:
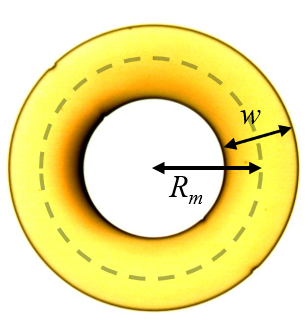
Break-up of toroidal films
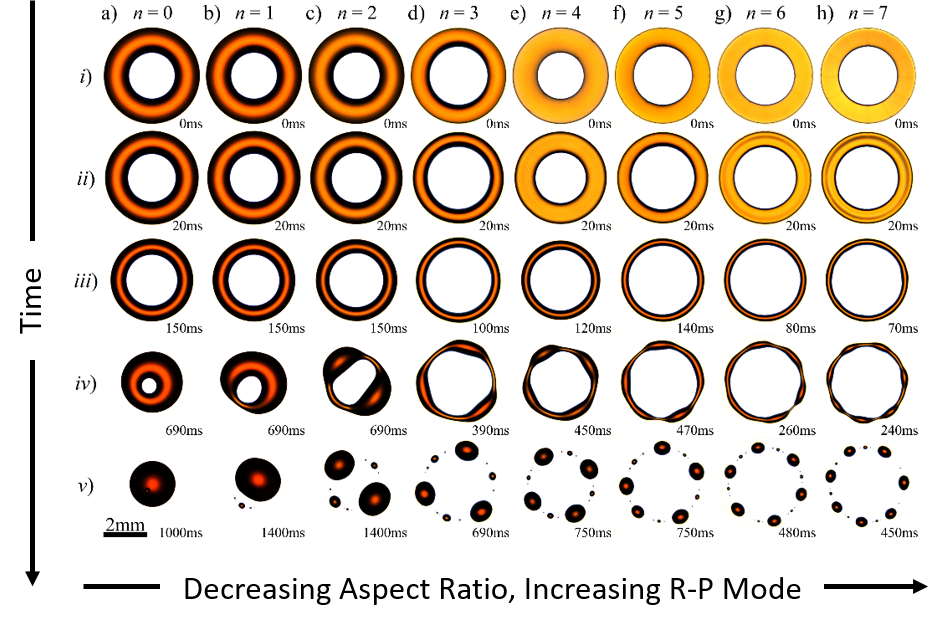
For the largest volumes, the fluid contracts into a single drop at the centre of the original toroidal shape. Any memory of the initial topology is lost. We define this to be a state n = 0. Smaller volumes result in a final pattern that princpally contains one or more drops, or nodes, positioned around the original toroidal shape. We call the number of nodes n.
An example with four nodes (n = 4) is shown below. Here, we can see that the liquid ends up mostly deposited in the four corners of a square shape, with some smaller deposits in between.
The cases of n = 0 to n = 7 are shown in the video below.
The image below illustrates the time evolution of the dewetting of different toroidal films. Here, the number of nodes increases from 0 to 7 as the volume in the film decreases. This is an example of the Rayleigh-Plateau (R-P) instability. Our technique allows us to select the breakup pathway and final state arising from the instability.
Publication
Controlling the breakup of toroidal liquid films on solid surfaces, A.M.J. Edwards, É Ruiz-Gutiérrez, M.I. Newton, G. McHale, G.G. Wells, R. Ledesma-Aguilar and C.V. Brown, Scientific Reports 11, 8120 (2021)
