Cheerios Effect on SLIPS
The Cheerios effect explains why objects that float on the surface of a liquid want to clump together. More specifically, objects that result in the liquid creating an upward-pointing meniscus want to clump together, as do those with a downward-pointing meniscus, whereas objects with opposite-pointing meniscii want to repel. This is illustrated schematically in the image below.
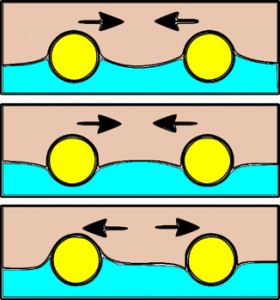
Objects will also want to clump to the edge of their container if the meniscus between the fluid and container curves in the same direction as that between the object and the fluid.
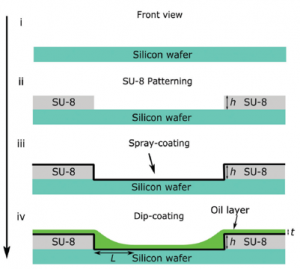
We can use the same concept behind the Cheerios effect to actively position droplets on a macro-patterned lubricant-impregnated surface. First we can pattern a Silicon wafer to contain “steps” using SU-8 photoresist. The pattern is then spray-coated and dip-coated in oil, as illustrated schematically below. The macro-patterning produces meniscii features in the impregnating liquid layer that interact with water droplets in a similar way to in the Cheerios effect.
To illustrate the concept, we constructed a V-shaped structure as a model system. A top view of the result is shown below.
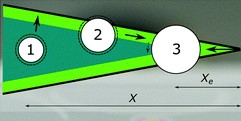
A drop in positions 1 is free to move in any direction across the surface without changing energy. However, if it gets close to the wall of the V-shape (to the area shaded light green in the image above), interactions between the meniscii of the drop and lubricating fluid cause the drop to be pulled towards the wall. Once it is at the wall (as illustrated by drop 2 above), the drop can move in either direction along the wall. The drop will not move away from the wall as this would require an increase in energy. If the drop moves such that it ends up at position 3, it will become pinned there. To move from this position in any direction would result in an increase in energy. A drop in this position is shown below.
Publications
- Drop transport and positioning on lubricant impregnated surfaces J.H. Guan, É.Ruiz-Gutiérrez, B.B. Xu, D. Wood, G. McHale, R. Ledesma-Aguilar and G.G. Wells, Soft Matter 13 (2017) 3404-3410.
- Droplet retention and shedding on slippery substrates B.V. Orme, G. McHale, R. Ledesma-Aguilar and G.G. Wells, Langmuir 35 (2019), 9146-9151